6.3. Calibration of a single parameter¶

6.3.1. Calibration using brute force¶

We will now calibrate the melt rate parameter with the brute force technique. Brute force means that we run the model multiple times, in a loop, each time with a parameter value taken from a predefined list of parameter values. The parameter values that gives the best fit with observed discharge is the ‘optimum’ value, i.e. the calibrated value.

But what is ‘best fit’? This can be defined with a goal function or objective function. Here we use the ‘mean squared error’:

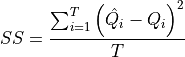
$SS = \frac{\sum_{i=1}^{T}\left ( \hat{Q_{i}}-Q_{i} \right )^2}{T}$

With, 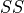$SS$ , the value of the goal function; 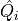$\hat{Q_{i}}$ , modelled streamflow at timestep 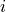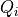$i$ ; $Q_{i}$ , measured streamflow at timestep 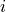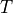$i$ ; $T$ , the number of timesteps.

Open runoff_calibration_one_par.py. Again it is the same script as runoff.py but the reports to disk have been removed. Have a look at the lower part now. There, the observed streamflow is first read from disk and stored as an array named streamFlowObserved. This represents the 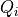$Q_{i}$ values in the equation above. The lowest part then calls the model (and passing the melt rate parameter value) which returns the modelled streamflow streamFlowModelled. At the bottom then the goal function above is evaluated for all timesteps. Note that it neglects the first year, which is the spin up time period required as snow cover is not yet realistic in this year.

If you run the model once, it prints the parameter value used and the objective function value.

Now modify the script such that it runs the model for a series of snow melt rate values, for instance from 0.0 up to 0.02, with a step size of 0.001. Note that you can first run it with a larger step and later on ‘zoom in’ to the correct value by narrowing the search range and using smaller steps. You will need to write a loop in Python, where you call the model each time with a different melt rate value. Store results in a text file and plot the response line, which is a plot of the parameter value (on the x-axis) vs. the goal function value (on the y-axis). The lowest point on this curve is the calibrated melt rate.

Question: What is the calibrated value of the melt rate parameter?

0.0089
0.0090
0.0060
0.0061

6.3.2. Effect of observations used in calibration¶

In the previous example you used the last three years for calibration. Let’s see whether using a subset of the data for calibration has an effect of the calibrated value.

Rerun the calibration but now calibrate on the discharge of the last year alone (instead of using the last 3 years).

Question: What is the calibrated value of the melt rate parameter, when calibrating against discharge for the last year only?

0.011
0.012
0.014
0.018